Lockdowns work.

You may have heard that they don't.

Most studies that come to this conclusion make one or more of the following mistakes

Use of case counts instead of growth rate

Most studies that look whether NPIs work tend to look at absolute case numbers (adjusted for population size) and try to correlate them with NPIs like stringency measures.

The core error made in this case is that NPIs don't affect the case numbers directly. Instead, they affect $R_t$, or the rate of spread of the virus. If you think about it, it makes a lot of sense: a person with COVID staying at home doesn't affect the current number of cases. They are still sick. What they do affect is how many people they are going to infect. By minimizing the amount of time and number of people they spend in contact with, they minimize the chances of transmitting the virus.

Why is this important? Lets say the following happens:

• A country starts with $R_t=2$. Their cases are growing
• They apply some interventions (lockdown). This gets them to $R_t = 1.5$

Now if we look at cases vs rate of growth, we get the following:

• The case graphs look about the same. Cases are still growing, so the measures applied "don't work"
• If we look at the rate of growth, we'll actually see that they work, but they're not enough to reverse the exponential process from growing to shrinking (For that we need $R_t < 1$).

So while looking at cases, we can't see whether measures are actually working until they're good enough to get $R_t < 1$

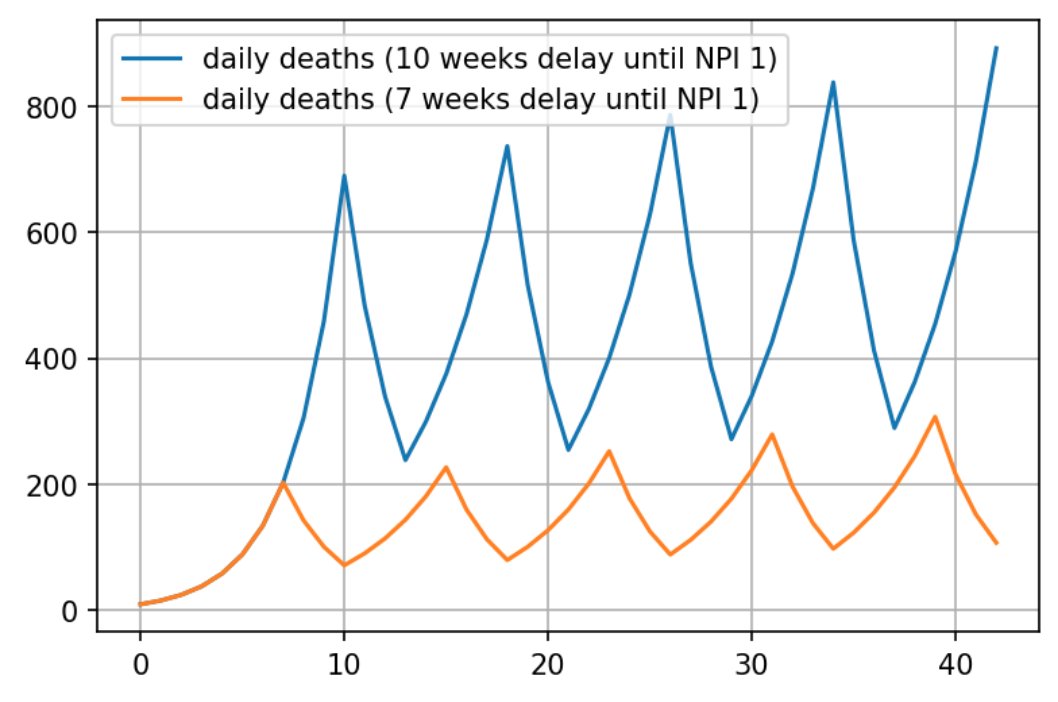
The situation is even worse if we look at case number totals. Then, the timing of the lockdowns also affects the outcome. A country that spends the same total amount of time in lockdowns but starts 3 weeks earlier could have vastly different outcomes than if they started later, because they let the "base" of the exponent accumulate:

Still, you might object - if that worked, we would still see a lot less virus in countries that have more stringent measures? The answer is no, but to figure out why, we need to get to the second problem, which is:

Comparing countries (multivariate problems as univariate)

As someone who has lived in 2 and visited (for an extended period of time) 3 countries in their life, we tend to underestimate just how different countries are, and how different the typical life of a person in those countries is. Variables include public transport vs cars, large supermarkets versus tiny shops, building ventilation codes, bar/pub ventilation codes, outdoors vs indoors venues, average household size, population density, climate and so on.

Comparing between countries is statistically futile. Its much better to compare the exact same place with itself before and after the introduction (or release) of NPIs (non-pharmaceutical interventions). That way, you can see what kind of difference that particular intervention makes, and you are no longer affected by any variables that are different across locations.

And we're down to the last problem, which is

Looking at stringency measures vs population behavior

A lot of studies measure various "stringency index" as the input variables. This is unfortunately also flawed. How effective a measure is will depend on a lot of things, including how much people believe in it. Convincing people that lockdowns don't work makes lockdowns less effective, for example. The fact that its Christmas or another religious holiday will also make people more likely to ignore decrees. Cultural factors could also be in play. Inability to stay at home due to lack of support from work might also play a role, and so on.

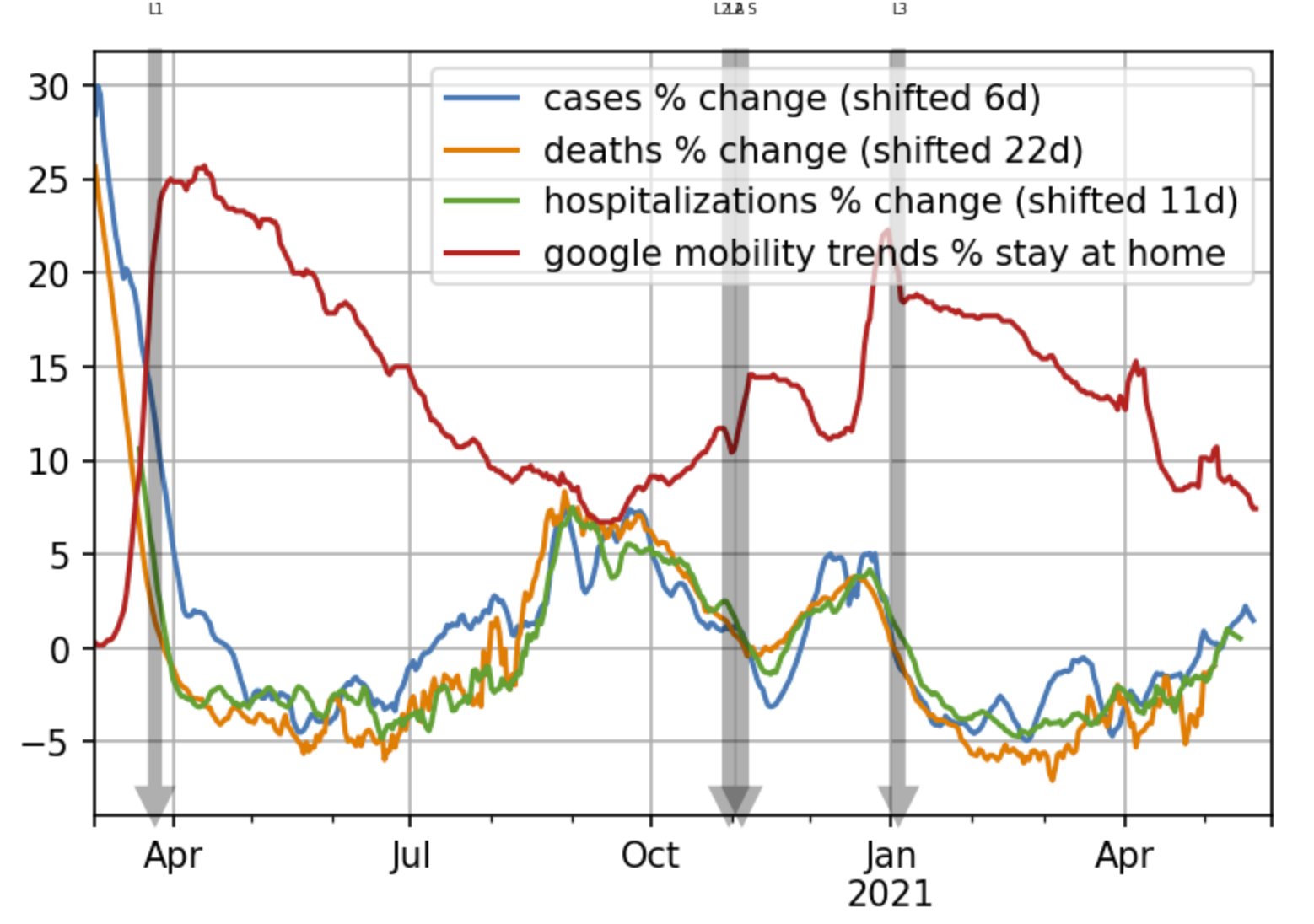
Its much better to measure real behavior. Google provides us with a variable called "percentage increase in stay at home time". The way they calculate this is by getting the baseline amount of time people spent at home daily around February 2020, then letting us know (for each country and each region) how much that time has increased or decreased relative to the baseline.

For example, if people in the UK stayed at home 14h/day at home on average in February 2020, and they now spend 20h/day at home, that is around 40% increase relative to the baseline.

This measure is not perfect. For one, outdoor activities are much safer than indoor ones but not counted as staying at home. For another, people in a country that have the habit of visiting each other a lot would completely skew the results. But its far less flawed than the stringency index.

Combining all corrections

If we combine all corrections, we get the following result for the UK.

Rate of growth (percentage change) of cases, hospitalizations and deaths is almost perfectly inversely proportional to the increase of time spent at home

Stats for more countries available at this link - you can see that people in Sweden, for example, did increase the amount of time they spend at home substantially

Stats for USA states available at this link